Last Updated on March 19, 2022 by QCity Editorial Stuff
Linear equations are one of the most basic concepts in mathematics. They are also some of the easiest to solve. Nonlinear equations, on the other hand, can be much more difficult to understand and solve. This blog post will explore how linear vs nonlinear equations work so you have a better understanding of each type.
A linear equation is an equation that looks like this: (2x+3) = 11. The variable x would then need to be solved for with 2x+3=11-x which equals 4x=6. So x equals 2 for this equation to balance out correctly! Linear equations can be solved by looking at both sides of the equal sign and solving for either side’s variables.
Linear equations can be solved by a variety of methods, but for most people, they are the easiest to understand. However, nonlinear equations cannot always be solved with these methods and require a different approach. This post will explore what linear and non-linear equations are as well as some strategies for solving each type of equation.
Comparison between Linear and Nonlinear Equations
| Parameters of Comparison | Linear | Nonlinear |
| Variable | Linear equations have one variable | Nonlinear equations have more than one variable |
| Algebraic method | Linear equations are solved using algebraic methods | nonlinear equations are solved using numerical methods |
| Constant slope | Linear equations have a constant slope | Nonlinear equations do not have a constant slope |
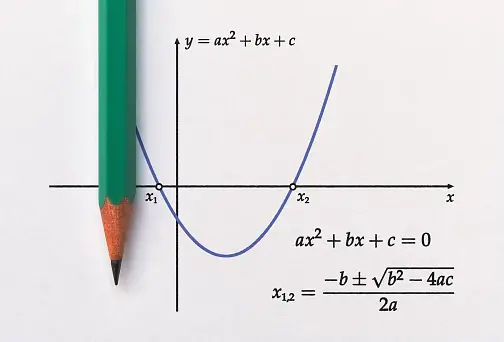
| Straight line | The graph of a linear equation is always a straight line | the graph of a nonlinear equation can be any shape |
| Zero | A linear function can never cross over itself or go below zero | A nonlinear function may cross over itself and may even go below zero |
What are Linear Equations?
Linear equations are used in mathematics to solve problems that involve two variables. When you have an equation with only one variable, it is called a linear equation because the graph will be a line. They can also be solved by graphing on paper or using technology.
These equations are considered basic concepts in algebra and pre-algebra classes, so understanding them is important for any student studying either of these subjects.
Linear equations are mathematical equation that is linear in form and has two variables. They can be written as either ax+by=c or y=mx+b. Linear equations can be solved by using the following methods: substitution, addition/subtraction opposite operations to combine like terms, adding/subtracting from both sides until one side becomes zero, multiplying both sides by a constant until one side becomes zero, dividing both sides by a constant until one side becomes zero.
There are many benefits of solving linear equations such as understanding what they mean mathematically and receiving hands-on practice with various techniques for solving them.
10 Differences Between Linear and Nonlinear Equations
1. Linear equations have one variable.
2. Nonlinear equations have more than one variable.
3. Linear equations are solved using algebraic methods, while nonlinear equations are solved using numerical methods.
4. The solutions to linear equations can be found by graphing the equation on a two-dimensional graph, while it is not possible to graph nonlinear functions without further information about the function’s behavior.
5. If you know the slope and y-intercept for a linear equation in standard form (y=mx+b), then you can find its solution by plugging the values into an equation like y=mx+b or 3x+2y=-7.
6. It is impossible to solve for x when solving for both variables in a system of linear inequalities; however, it is possible if there are only two variables in the system of inequalities.
7. Linear equations have a constant slope.
8. Nonlinear equations do not have a constant slope.
9. Nonlinear equations may be written in the form of y = f(x) or y = g(x), depending on their shape and equation type.
10. If you graph linear and nonlinear functions, linear graphs will look like lines while nonlinear graphs will look more curved.
Interesting Statistics or Facts of Linear Equations
1. Linear equations are used in many different fields, such as engineering and physics.
2. A linear equation can be written in slope-intercept form with the following formula.
3. The graph of a linear equation is always a straight line when graphed on an x-y axis.
4. All points on the line have coordinates that satisfy the same linear equation.
5. Different types of graphs can be created with lines by varying coefficients and intercepts.
6. Lines can also be used to represent functions or inequalities in mathematics, such as y = 2x + 3 for example.
Interesting Statistics or Facts of Nonlinear Equations
1. Nonlinear equations are used in many fields of study.
2. Linear equations can be solved by graphing them, but nonlinear equations cannot.
3. The graph of a linear equation is usually a line that intersects with the x and y-axis; the graph for a nonlinear equation will not follow this pattern.
4. One example of an application for nonlinear equations is calculating how much money you would need to save each month if you want to retire with $1 million at age 65.
5. If someone were to invest $200 per month at 12% interest, they would have around 1 million dollars after 34 years.
6. To find out how much money someone needs to save each month to retire with 1 million dollars at age 65, they would take their desired monthly income ($40K) and divide it by 1 – (their assumed annual rate of return). This gives them 1667/12 = 140 which is what they should be saving every year.
Conclusion
Nonlinear equations are more difficult to solve than linear equations. The difference between these two types of equations is the number and type of operations that must be performed in order to find an answer, as well as what form they take (algebraic or transcendental). Linear equations always consist of one operation which can be solved with a simple substitution. Nonlinear equation sets usually require multiple steps for solving, such as Newton’s Method. These methods tend to have many “dead-ends” where it seems impossible to continue on your way towards finding an answer, but you need only keep going through all the possible solutions until you reach a final result. Learning how nonlinear functions work is just another step in understanding mathematics.
References:
Resource 01: https://en.wikipedia.org/wiki/Linear_equation
Resource 02: https://www.vedantu.com/maths/difference-between-linear-and-nonlinear-equations